Week 5: Embodying Common Multiples

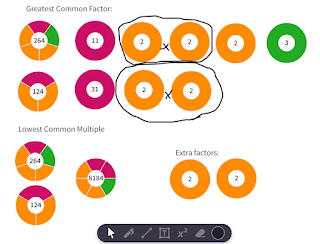
 I always have two teenaged boys in my house (three if you count my dog Georgi). This week, I had four. Two of them are taking Math 10 and would like to start on the right foot. So there I was: at the kitchen table helping them simplify equations (expressions?), earnestly trying to reactivate those long-atrophied high school math muscles of mine. At the heart of many of their woes were foundational ideas about factoring, multiples, and fractions. I attempted to illustrate rules for finding GCF and LCM using prime factor circles on Mathigon's Polypad like so: 

Prime factors circles are handy for modeling (and finding) both LCM and GCF, although conceptually still abstract. They do not provide insight into where one might encounter LCM an GCF situations, what they might look, or sound, or feel like. That is why I was so excited to see Sarah Chase's explorations of repeating number patterns using body movements. When do body movement patterns meet up at the beginning of a new sequence? At the common multiples! Why are repeating patterns of 6 and 8 not as complex and interesting as repeating patterns of 7 and 9? Because 6 and 8 share a common factor of 2 and have an LCM of 24. 7 and 9 share no common factors and have an LCM of 63. 

You can feel it, too. Here is a simple exploration of repeating patterns of 3 and 4 versus a repeating pattern of 2 and 8:

The 3 and 4 dance was much trickier (and more interesting) than the 2 and 8 dance. I decided to explore the patterns using grid paper and number lines as well: 

I was working away at these during the intermission of the Leafs vs Canucks game at Rogers Arena. I apologize for the lack of colour. I tried to use texture and a combination of dull pencil and dying pen to illustrate the differences in complexity of pattern. It definitely is there: the 2 and 8 pattern is boring compared to the 3 and 4 pattern. 

Here is the number line exploration: 

Note a third pattern that I was going to dance. It is yet to come.

You can hear the difference, too. I tried two other number combinations: 4 & 5 and 6 & 9. 4 & 5 share no common factors. 6 and 9 share a common factor of three and have an LCM of 18. How might they sound when you clap these combinations? Have a listen:

In my opinion, the tighter 4 & 5 is more interesting (it was certainly more interesting to clap), but both would have benefitted if each number had been a different note and you couldn't hear me counting out loud :)

Now, what I loved about this exploration of common multiples is the options for sensing just what they are. The grid and number line representation should be common in math classes. One is more likely to see the number line representation in textbooks. However, I'm not sure how often students are allowed to play around with either. I think that a lesson sequence with the intention of helping students make sense of common multiples should definitely include some pattern play with both models. 

The clapping and dancing explorations were the most fun. I think that clapping common multiples is a very accessible, low-stakes way for students to sense common multiples. If I had access to hand chimes, I might use those in place of hands, just to add another sound dimension to the experience. The dancing exploration would be challenging for students, but might be an interesting extension for some. I would certainly show the video of Sarah Chase and have students to give the 2 & 3 pattern sequence a try. 

So how about a possible teaching sequence? I would likely start with simply exploring the idea of multiples as repeating patterns. I think the 10 x 10 grid is an interesting way to visualize the patterns. I like the idea of simple repeating steps to embody patterns of simple multiples as well: step, step, step, turn or step, step, hop! 

Next, we would begin to explore common multiples using the models I outlined above, starting with number lines and grids, and ending with clapping and dance. 

Reading Connections:

I didn't like all of the articles this time. I found the Kelton & Ma (2018) article unnecessarily wordy and complicated for what it ended up being: a summary of how two lessons went. I thought both ideas were interesting, although would have preferred seeing them in video form. The first group's revelation that you could pivot the whole group in a circular form around the centre student in order to end up on your opposite position on the number line was neat. However, there were only 11 students participating and I'm not entirely sure what helpful insights were gained by these grade 8 students moving on a giant number line. It was clear that there was some initial goofing around. How long did that last? How seriously did any of them take the idea? Same with the whole-half activity. I would have loved to see the whole class in action, management issues and all. Finally, I wish both studies had included post-activity interviews with the students about their learning. 

The Dietiker (2015) article was interesting. I love the analogy of story: mathematical objects and operations as characters and actions, and structures for interacting with ideas as settings. The most helpful idea is the notion of creating thought engagement through plot by playing with the tension between what students anticipate and what they experience mathematically. Even this past week with my two grade 10 boys, we were experiencing 'plot tension' in our efforts to simplify equations, although not enjoying it: Did we do it correctly? Maybe. Check the back of the book! Nope...DAMN! I know that the author did not mean this type of frustrating plot tension. Dietiker had a great example of a probability game and a surprising/fun plot twist. However, I wonder if the former type could still be approached more productively and enjoyably, especially since it happens all of the time. I used to play with the tension of product estimation (and solution via calculator) in 2 x 2 digit multiplication and anticipated way of solving 2 x 2 digit multiplication questions when students were first learning the method. 2 x 1 digit multiplication is so much less complicated and sets up an expectation that 2 x 2 digit multiplication follows the same pattern when it does not. Students actually had fun at the start trying to figure how on earth it was done and why it was done that way. When they were finally exposed to various models for solving, they were paying with rapt attention. 

The Riley et al. (2017) article is a gem: well written, clear examples and methods, decent sample size, and interesting results. This is one that I am going to get my team (of numeracy support teachers) to read. I'm always on the lookout for ideas that might appeal broadly to teachers of all stripes. This year, our focus was on games in K-10 math...very popular and productive, even with teachers who are staunch textbook followers. After reading the Riley et al. article, I think that math learning in connection with physical activity might also be of that ilk, even if they did admit that a limitation of the study was that the teachers involved were keen to give it a go. I will be dipping into it more! Very curious about their PD model. 

My job today is to figure out how I am going to choreograph my final dance: repeating patterns of 2, 3, and 8. I keep reminding myself that I only have to make it to 24.